Santa Fe Institute 2006
Graduate Workshop in Computational Social Science Modeling and Complexity
Homework 1: Optimal Group Size in Aircraft Boarding?
Nils Bertschinger and Mary
Shenk
Model Overview
Goal: Efficient (quicker) boarding of aircraft.
Optimizing: Costs of Airline, Comfort of Passengers
General
Assumptions:
§
Perfect order of seating
yielding quickest time to departure.
§
Perfect seating order
begins in rear of aircraft and moves forward row by row.
Main Variables:
1. Time outside the aircraft (boarding)
2. Time inside the aircraft (seating)
Initial Formula (for
boarding and seating time when passengers enter plane in groups of size
g):
[b(g)g + s(g)g] N/g =
[b(g) +s(g)] N
Where:
b(g)
= boarding time per person when boarded in a group of size g
s(g)
= seating time per person when in a group of size g
g =
group size
N =
number of passengers (100)
Outcome: minimize time per person (plotted on y axis)
on group size (plotted on x axis)
Boarding
Boarding procedure
(model assumptions):
§
Agent calls group of
people for boarding.
§
Members of group enter line
based on distance from ticket checking area. Walking times are assumed to be
uniformly distributed between 0.5 and 2.
§
Fixed time of ticket
checking = 0.2 units.
§
As soon as someone is
getting faster to the line than ticket checking occurs for the person before
her, a line forms.
§
When a queue forms, time
to boarding becomes linear, since everyone has to wait for the person before
her to be boarded and is then boarded in a fixed time (see above).
Results:
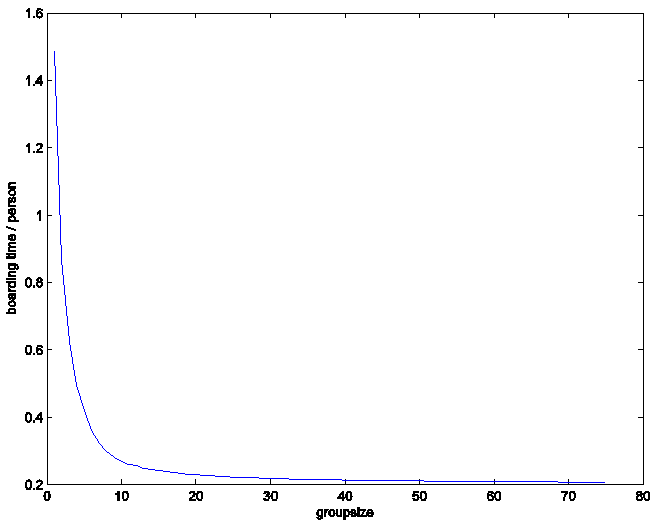
As groups get larger, boarding time per person
approaches the fixed amount of time for ticket checking. This is due to queue formation, which absorbs
much of the variation in travel time which affects the boarding time per person
for small groups. These findings
indicate an ideal strategy of seating the entire plane as one large group
(considering only boarding time).
Seating Version 1:
Seating within Groups
Position numbers refer
to a person’s place in the ideal boarding order, ranging from 1-100 starting in
the back of the plane. The order of position
numbers within groups is assumed to be random since people arrive according to
their place in the waiting area as described in the section on boarding.
Seating procedure 1:
§
The person first in line
is seated while anyone with lower position numbers (and those behind them) are
blocked from seating and forced to wait.
§
Anyone with a higher
position number than the first person in line can be seated unless they are
blocked by a lower number person.
§
Once the first person
and those with higher position numbers are seated, the cycle repeats with the
next person in line as the first person.
§
It takes a fixed amount
of time for one person to seat (1 unit).
§
People who seat in one
cycle all sit in parallel (no lag).
Example of how algorithm
works
§
2 3 1 5 4 ... (position
numbers of people entering the plane (round 1))
§
2 can sit since she is
the first person in the line
§
3 can sit since she has
a seat behind 2 and is therefore not blocked
§
1 and all persons behind
are blocked by 3
§
therefore 2 and 3 sit
down in parallel in round 1, all others have to wait
§
1 5 4 ... (position
numbers of people not seated after round 1)
§
1 and 5 can sit down in
parallel in round 2, whereas 4 (and all persons behind are still blocked)
§
4 ... (position numbers
of people at the beginning of round 3)
§
...
Same in shorter notation
that will be utilized later:
§
2 3 1 5 4 ...
§
s s|1 5 4 ...
§
1 5 4 ...
§
s s|4 ...
§
4 ...
Results:
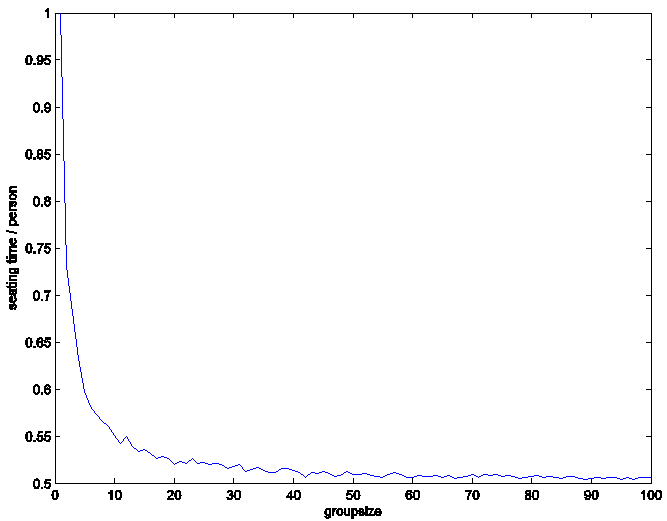
As group size increases, average boarding time per
person approaches 0.5 units. This
decrease is most likely due to the increased likelihood of parallel seating in
larger groups. These findings indicate an ideal strategy of seating the entire
plane as one large group.
Seating Version 2: Seating Groups in Semi-Parallel
Idea:
§
Group 2 is called as
soon as Group 1 has passed ticket checking so they are in line directly behind
Group 1.
§
Group 2 only waits in
the aisle while Group 1 is still larger than ‘l’ persons. When group 1 becomes
smaller they stop blocking Group 2’s seating area. This parameter can be interpreted as a
measure of the amount of space available on the plane (e.g. number of aisles,
width of aisles).
The same boarding
procedure as above is used, but instead of calculating the average time it
takes to seat the whole group, we estimate the average time until a group
becomes shorter than ‘l’ persons.
Results:
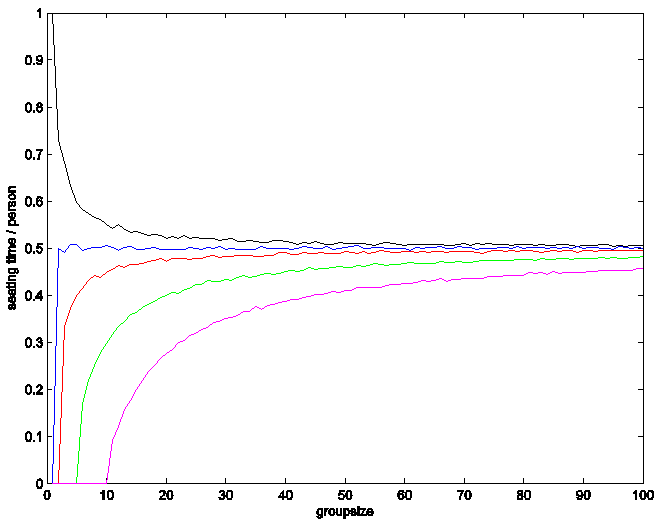
The black line on the top part of the graph
indicates the results for l = 0, which are the same as the results discussed
above. Lines for l = 1, 2, 5, and 10
appear successively on the bottom half of the graph. These results indicate that the longer the
line can be before blocking the next group from seating, the more quickly
seating will occur. This is a clear
reversal of the patterns found in previous simulations, and suggests an ideal
strategy of individual or small group seating.
Total Time to Board and
Seat
When run in parallel,
the boarding algorithm usually takes much less time to run than either version
of the seating algorithm and thus dominates the results. Because of this, we decided to concentrate on
seating algorithms as the key determinants of the speed at which a plane can be
boarded.
Seating Version 3:
Seating Groups in Blocks
Our previous simulations focused on the dynamics
of single groups and the interactions between groups. Since the idea presented above can model the
group interactions only to a limited degree, a more realistic way to approach
the problem is to run the model described above with the prescribed number of
100 passengers organized into blocks of size g. Passenger positions are
randomized within blocks, but not between blocks.
Results:
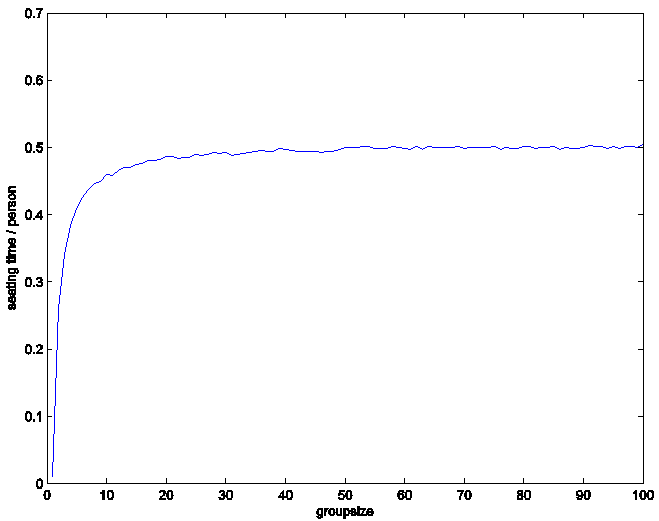
These results indicate that average boarding time
increases with group size, once again suggesting an ideal strategy of boarding the
plane individually or in small groups.
Seating Version 4:
Seating Blocks in Parallel
Algorithm:
Same
as before, except:
§
Parallel seating is
allowed if the passenger’s position (s) is sufficiently far away from the
person blocking (b) the passenger.
§
We take into account the
number of people waiting in the aisle between person b and person s (x) and a
factor (l) modeling the amount of space in the plane.
Example of how the algorithm works (for l = 2):
§
2 3 1 5 8 9 6 ...
§
s s|1 5 s s 6 ... 1
is blocked, since 3 > 1
5 is blocked, since she not sufficiently far away from 3:
x = 1, since 1 is waiting in between
difference of
positions (5 – 3) is not larger than l x
= 2
8 can sit, since she is sufficiently far away
from 3:
here, x = 2,
since 1 and 5 are waiting in between
(8 – 3) > l x = 4
9 can sit, since 8 < 9
6 is blocked, since 9 > 6
§
1 5 6 ...
Results:
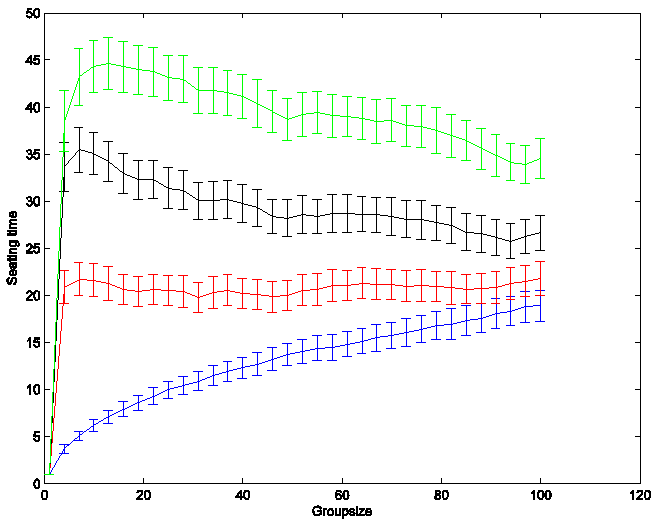
The lines above represent the effects of parallel
seating of blocks with successively higher measures of space in the plane
(l). Blue represents l = 1, which is
similar to the results above in suggesting that small boarding parties are more
efficient. However, successive values of
l (2, 4, and 10) indicate the increasing efficiency of larger boarding
parties. Here the ideal strategy regarding
boarding party size is dependent on the number of passengers in one group who
can stand in line without blocking the group behind them. Perhaps obviously, these results also
indicate that planes with roomier or multiple aisles (low values of l) are
likely to board more quickly in general than those with less space for waiting.
Seating Version 5:
Seating Blocks in Parallel with Cheating
This final version of our seating algorithm explores
the results of ‘cheating’ by passengers who do not board the plane with their
assigned blocks but instead join the queue randomly.
Algorithm:
§
Same as before, except a
small fraction (p) of passengers are randomly assigned new positions in the queue
without respect to their block membership.
§
The factor indicates the
likelihood of cheating; small factors mean less cheating while large factors
indicate more.
Results:
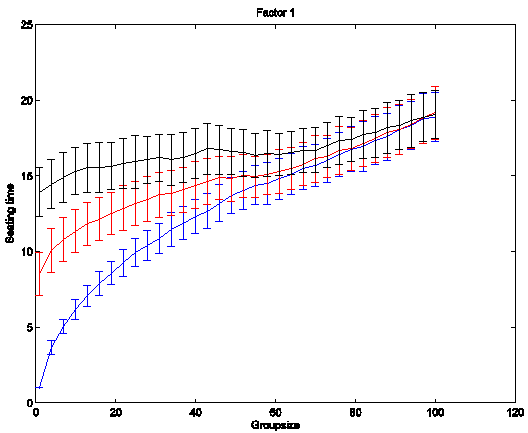
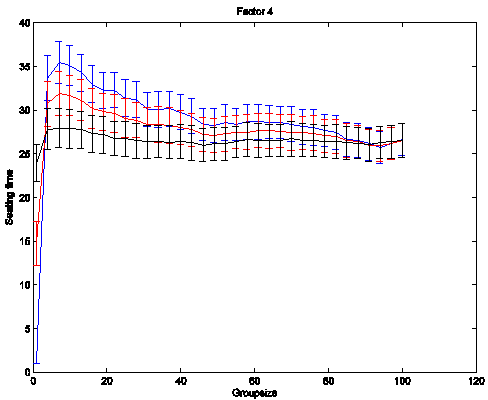
From these two sample graphs showing results for l
= 1 and l = 4 we can tell that higher rates of cheating move the boarding time
towards the time required for a large group since the group structure gets
perturbed. The blue line in each graph
represents 0 cheating, the red line indicates p = .2, and the black line
indicates p = .5.
Summary
Our simulations showed
that boarding time did not seem to be a major bottleneck factor. As soon as queues are formed, it becomes
efficient. Seating time showed much more
promise as a factor in efficient loading of an aircraft, however most of our
results indicated that either very small boarding groups (individuals) or very
large boarding groups (100 passengers) were most efficient. In general, calling the passengers in groups
did not show meaningful effects.
Conclusions
Either:
a) We have errors in computation we haven’t found, or
b) Our model isn’t as sensible as we think it is, or
c) We are missing some key factors in our simulations,
or
d) Boarding group size really doesn’t matter and the
airlines simply employ them for inscrutable reasons of their own.
Future Directions
Our model
could (easily) be improved to incorporate row and column structure of the seat
layout by using a suitable position numbering scheme. Further extensions could involve incorporating
baggage storage and passenger walking speed.
However, an alternative approach is also suggested by our model. The abstract approach relates the problem of
boarding a plane to the mathematical problem of finding an incomplete (here a
group-structured) ordering that optimizes a certain performance measure (here
seating time) that depends on sequence order. This might allow for analytical
investigations as compared to the simulation results presented here.